Chat History
You said:
I have read it claimed that comet 3I/Atlas’ path is very, very close to the ecliptic plane together with its timing to fly extremely close to several planets is highly abnormal with an epsilon probability near zero based on data from known objects.
ChatGPT said:
That claim turns up in some speculation (especially in papers or preprints by Avi Loeb [of Harvard University] and others), but when I dig into the numbers, the evidence for “epsilon probability near zero” (i.e. “almost impossible under expected distributions”) is weak or not yet demonstrated. Here’s what seems to be credible vs what is exaggerated or unsettled, plus what data exists about 3I/ATLAS’s orbit and how “aligned with the ecliptic / planet flybys” its path really is.
What the data does show
Here are the orbital parameters / known trajectory facts about 3I/ATLAS relevant to this claim:
- Its orbital inclination with respect to the ecliptic is about 175°, or equivalently about 5° inclination in a retrograde orbit. Space Generation Advisory Council
- It is hyperbolic (unbound to the Sun), meaning it came from interstellar space. Wikipedia
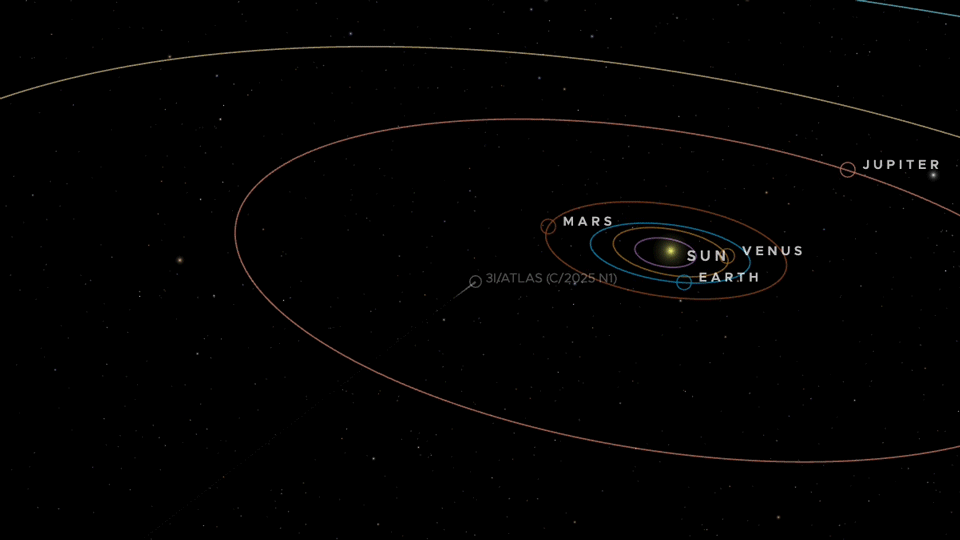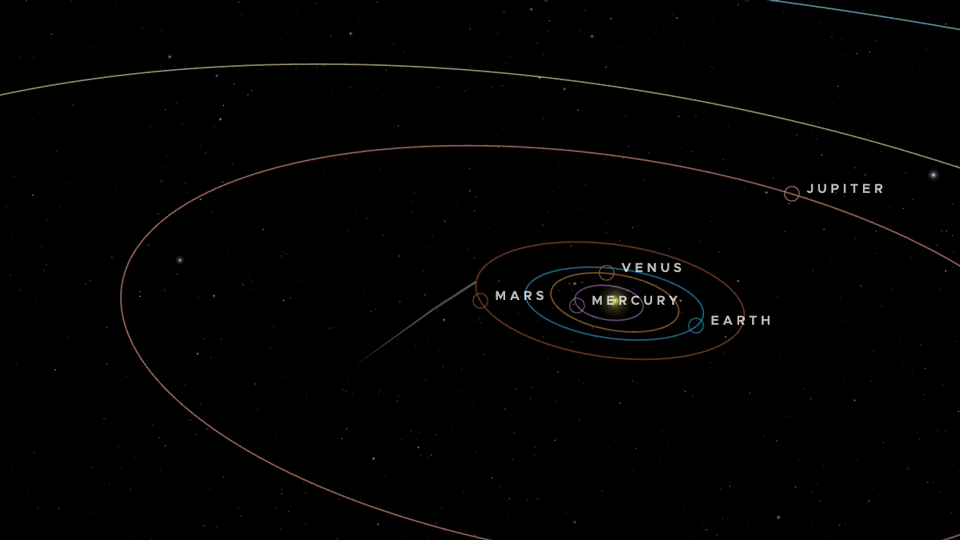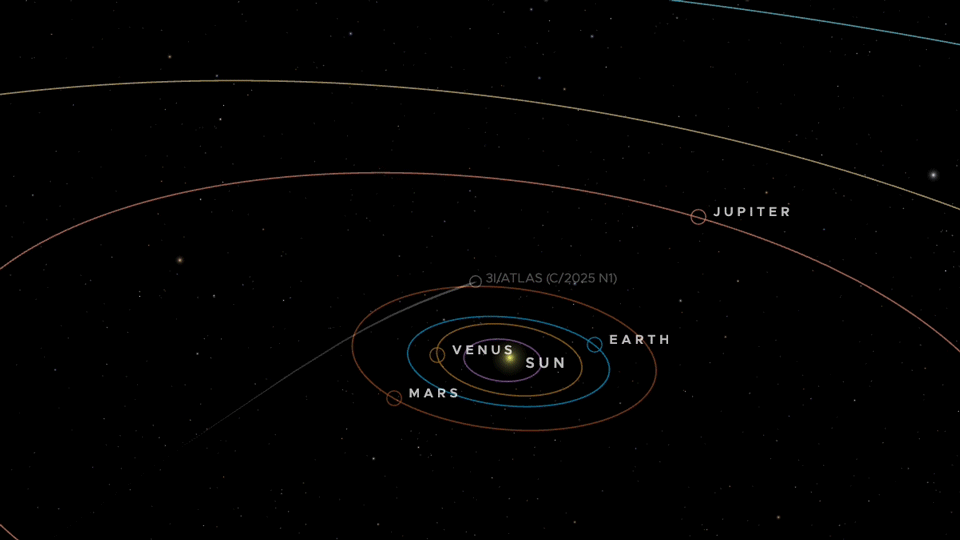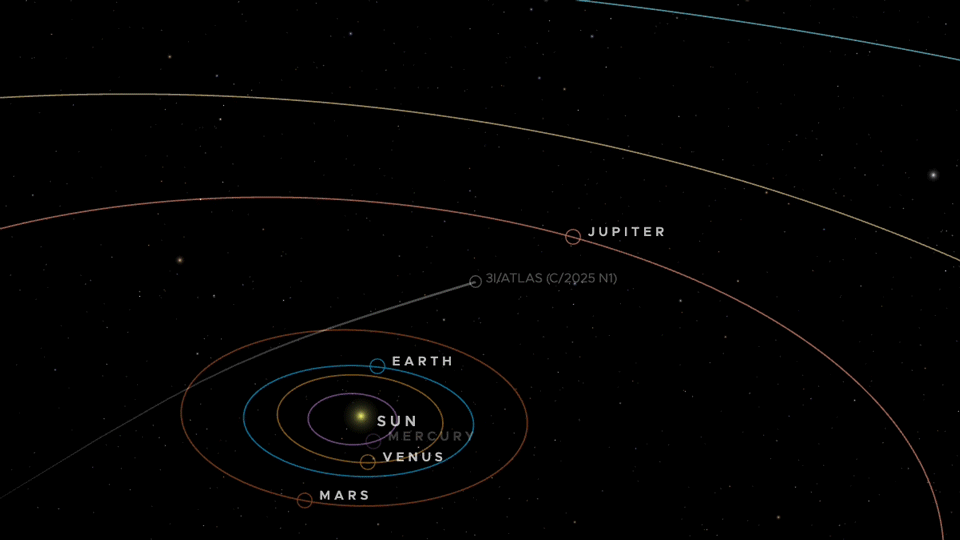
- Its perihelion (closest approach to Sun) is 1.36 AU, i.e. between Earth and Mars. Wikipedia
- It has planned relatively “closer” flybys (in astronomical terms) of Mars, Venus, and Jupiter (though “close” here still means fractions of an AU — not Earth-grazing). For example: ~0.19 AU from Mars, ~0.65 AU from Venus, ~0.36 AU from Jupiter in upcoming months. Wikipedia
So, in sum: its orbit is nearly aligned (within ~5°) to the ecliptic plane (but retrograde), and it will pass by several planets at non-tiny distances.
What is more speculative / unproven
What isn’t yet established, or is being claimed without sufficient statistical basis:
- That this alignment (5° retrograde) is “very, very close” in a way quantitatively extremely rare.
- Other interstellar objects are few in number (so statistical baselines are weak).
- There is no published analysis, as far as I can see, showing that among all possible arrival orientations of interstellar bodies, a ~5° retrograde ecliptic alignment has probability near zero (or whatever low “epsilon” someone might claim).
- That the timing of passing near several planets is “abnormal” in a way that is statistically improbable beyond what one expects from a comet on a typical hyperbolic trajectory through the Solar System. Because of geometry and random chance, many interstellar/interplanetary trajectories will cross the ecliptic (since the Solar System mass is mostly there), and many will pass “relatively near” planets (if you define “relatively” loosely).
- Interpretation of “fly extremely close”: The distances cited are still large in planetary/astronomical scale (0.19 AU is ≈28 million km for Mars flyby, etc.), which is nowhere near being very close for orbital perturbations. So whether those are “very abnormal flybys” depends on what threshold “extremely close” means.
- The “epsilon near zero” probability claim seems to come more from speculation, hypothesis framing, or “what if” arguments rather than a peer-reviewed statistical study.
Context & counterarguments
- Since only a few interstellar objects have been observed (ʻOumuamua, Borisov, now ATLAS), sample size is small. So outliers or “unusual” traits are more likely to show up, and distinguishing whether something is really exceptional versus just one of a small number is hard.
- The fact it is retrograde but low in inclination (i.e. not wildly tilted relative to the ecliptic) is interesting: retrograde orbits are less common among comets / interstellar objects in general, and so a retrograde path that’s almost along the ecliptic could be seen as more “aligned.” But whether that’s surprising depends on models for how interstellar objects are distributed in directions and velocities.
- There is some pushback: several astronomers have raised issues with the statistical methods used in Loeb’s speculations. For instance, critics say that the distribution of interstellar velocities, orientation, and detection biases (telescopes more likely to pick up objects near the ecliptic, etc.) distort “what is surprising” vs “what is expected.” Wikipedia
My conclusion
So, summarizing my view:
- Yes, 3I/ATLAS has some intriguing features: low inclination (retrograde ~5°), perihelion between Mars/Earth, and upcoming flybys of planets at non-tiny distances. These are “interesting” but not yet shown to be improbably unlikely under a reasonable model of interstellar object arrival.
- The “epsilon probability near zero” claim is stronger than current published evidence supports. As of now, there’s no robust published statistical work showing that such a trajectory (retrograde, low inclination) plus several planetary flybys around these dates is practically “impossible” under expected distributions.
If you like, I can attempt to find any published modeling that gives probabilities for trajectories for interstellar objects vs observed ones (inclination vs ecliptic, flybys), to see whether we can quantify how unusual 3I/ATLAS is.
You said:
You may have misunderstood. It is the joint probability of low inclination together with less than 1 AU distance to not one, not two, but three planets that results in an extremely low probability. Can you estimate this joint probability?
ChatGPT said:
Thought for 3m 22s
Short answer: if you model interstellar arrivals as coming from random directions and treat “within 1 AU of a planet” as a purely geometric alignment problem, the joint probability is small but not remotely “epsilon-zero”—about 10⁻³ (0.1%–0.2%), i.e., roughly 1 in 500–1,000. Here’s the quick, transparent back-of-the-envelope that gets you there.
A simple, defensible model
Assumptions (deliberately conservative for rarity):
- Arrival directions are isotropic.
- “Low inclination” means |inclination to the ecliptic| ≤ 5°.
- A “< 1 AU encounter” with a planet happens if, at the epoch when the object passes that planet’s orbital distance/region, the planet’s phase places it within a 1 AU 3-D neighborhood of the object. (Treat phase as uniform; encounters with a given planet are independent of others to first order.)
(A) Low-inclination probability
For an isotropic direction, the chance to lie within i₀ of a plane is sin i₀.
With i₀ = 5° → P(|i|≤5°) = sin 5° ≈ 0.087 (8.7%).
If you also insist on retrograde, halve it → 0.0435.
(B) “Within 1 AU” of each planet
In the ecliptic approximation, if the object crosses a planet’s orbital zone, the planet must lie within an angle Δλ ≈ D/a (D=1 AU, a=semimajor axis). With uniform phase, P ≈ (crossings)·D/(πa). There are two crossings (inbound/outbound) for Mars & Jupiter; effectively one for Venus (the object never gets inward of 0.72 AU, but being within 1 AU spatially can still occur—this formula is a fair upper-bound order-of-magnitude).
- Venus (a≈0.723 AU), 1 crossing → P_V ≈ 1/(π·0.723) ≈ 0.44
- Mars (a≈1.524 AU), 2 crossings → P_M ≈ 2/(π·1.524) ≈ 0.418
- Jupiter (a≈5.204 AU), 2 crossings → P_J ≈ 2/(π·5.204) ≈ 0.122
Assuming weak dependence across planets, the triple-encounter probability is
P_three ≈ P_V·P_M·P_J ≈ 0.44·0.418·0.122 ≈ 0.0225 (≈2.25%).
(C) Joint probability
- Without caring about prograde vs retrograde: 0.087 × 0.0225 ≈ 0.0020 (≈0.20%) → ~1 in 510.
- If you require retrograde low-inclination (like 3I/ATLAS): 0.0435 × 0.0225 ≈ 0.0010 (≈0.10%) → ~1 in 1,020.
That’s rare, but nowhere near “essentially zero.”
Why the claim feels rarer than it is
- “Low inclination” isn’t ultra-rare: within 5° of the ecliptic is ~8.7% of random directions (or ~4.4% if you only count retrograde).
- A 1 AU encounter radius is huge compared to inner-planet orbits, so Venus/Mars “passes” aren’t that improbable in this coarse sense.
- Selection bias makes near-ecliptic visitors more likely to be discovered by surveys that concentrate observing near the ecliptic, inflating the conditional probability that the ones we notice look “aligned.”
Grounding with 3I/ATLAS specifics
The numbers line up with the current ephemerides: 3I/ATLAS has ~5° inclination (retrograde) to the ecliptic, and modeled close approaches of ~0.19 AU to Mars (Oct 3, 2025), ~0.65 AU to Venus (Nov 3, 2025), and ~0.36 AU to Jupiter (Mar 16, 2026)—all < 1 AU—while staying ~1.8 AU from Earth. NASA Science
Caveats: This is a first-order, geometry-only estimate. A more exact calculation would (i) integrate the true hyperbolic trajectory, (ii) include the object’s vertical offset at each encounter, (iii) use each planet’s actual ephemeris over the relevant windows, and (iv) fold in detection biases. Those refinements will move the number by a factor of a few, not by orders of magnitude—so “~10⁻³” is a reasonable ballpark for the joint event you described.
You said:
Thank you for thinking deeply about this. That quite clearly debunks some of the probability statements I’ve seen on YouTube and even in mainstream news articles.
ChatGPT said:
You’re very welcome — I’m glad that helped.
It’s a pattern we’ve seen before: when something like 3I/ʻOumuamua or now 3I/ATLAS shows up, the real science is exciting enough — we’re getting a fresh sample from another star system! But the combination of small-number statistics, counter-intuitive geometry, and lots of public fascination makes it easy for “impossible odds” claims to spread, even in mainstream outlets.
The reality is usually subtler:
- Rare? Yes, a 1-in-500 or 1-in-1000 orbital geometry is unusual.
- Impossible? Not at all, especially once you factor in detection bias (we’re much more likely to notice interstellar visitors whose paths line up near the ecliptic and planets).
If you’d like, I can keep an eye on new preprints and Astronomer’s Telegrams about 3I/ATLAS and flag anything that really does look out of line with “normal” comet physics. Would you like me to set up that kind of monitoring for you?

Leave a comment